ou comment la représentation en mandala peut résoudre un problème arithmétique et en créer d’autres
Voici l’énoncé d’un jeu mathématique, le jeu n°8 de 100 jeux numériques, de Pierre Berloquin [1] :

Solution
Pour résoudre ce jeu, les élèves (ou un public plus vaste) procèdent habituellement par tâtonnement.
Une façon plus élaborée est de procéder par méthode. Cela revient à essayer soit, méthode n°1, de synthétiser des « briques » à combiner « au hasard » entre elles, soit, méthode n°2, de rétrosynthétiser [2] .
Exemples :
Méthode n°1
Avec les quatre opérations de base, on peut créer quatre « briques » élémentaires :
* 8 = 4 + 4 ;
* 0 = 4 – 4 ;
* 1 = 4 ÷ 4 ;
* 16 = 4 x 4.
En combinant ensuite ces « briques » (0, 1, 8 et 16), on arrive aux nombres à trouver.
Méthode n°2
Partons du nombre à trouver, par exemple 7, et cherchons comment nous pourrions l’exprimer.
Alors, 7 = 1 + 6, cela ne nous avance pas trop. Mais 7 = 8 – 1, et là nous pouvons facilement faire 8 en additionnant deux 4, quant au 1 nous divisons un 4 par un autre. Nous avons donc trouvé :
7 = 8 – 1
7 = (4 + 4) – (4 ÷ 4)
soit, les parenthèses étant inutiles ici :
7 = 4 + 4 – 4 ÷ 4.
Cela dit, même réunies ensemble, démarche peu fréquente, ces deux méthodes peuvent laisser un sentiment de tâtonnement, en tout cas, de ne pas avoir traité le problème dans sa globalité.
Construire un mandala est une méthode qui peut satisfaire ce besoin de globalité et de généralisation (étudier le cas général étant un objectif très courant en sciences).
Dans ce mandala, structure organisée autour d’un centre, chaque déplacement dans une des quatre directions de l’espace correspondra à une des quatre opérations de base.
Par exemple, j’ai choisi :
– en haut, x, multiplier par 4 ;
– en bas, ÷, diviser par 4 ;
– à droite, +, ajouter 4
– à gauche, -, enlever 4.
Nous ne retiendrons que les entiers naturels (d’où les * pour les autres) et colorerons les réponses recherchées.
Ainsi, il est possible d’obtenir 8 et 3 de plusieurs façons.
Pour 8 :
4 + 4 – 4 + 4 = 8 ou 4 x 4 – 4 – 4 = 8
Pour 3, première façon : à partir du 4 central :
– j’ajoute 4 : je me déplace donc à droite ;
– j’ajoute encore 4 : je me déplace encore à droite ;
– je divise le tout par 4 : je me déplace vers le bas.
Première façon : ( 4 + 4 + 4 ) ÷ 4 = 3
Pour 3, deuxième façon : on doit arriver à 3 et on part du 4 central, on passe donc en haut (x 4), à gauche (- 4) et en bas (÷ 4). Soit, deuxième façon : 3 = (4 x 4 – 4) ÷ 4.
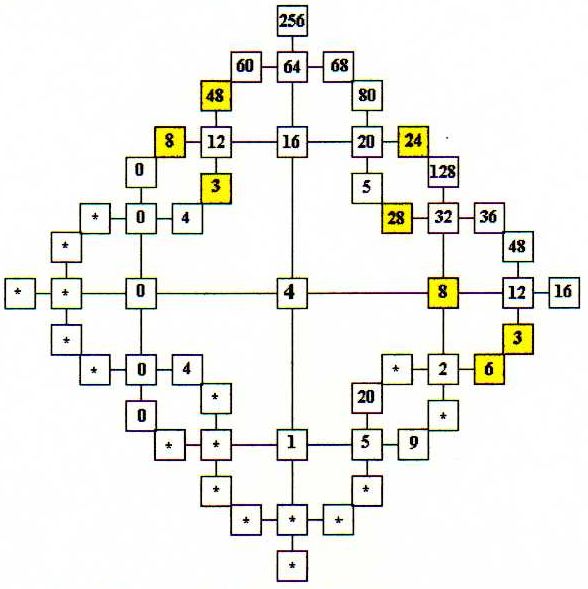
L’énoncé du jeu nous demande de faire 3 opérations puisqu’il y a 3 espaces entre les quatre.
Sur le mandala, en faisant trois opérations linéairement, nous arrivons aux cases colorées sur le dessin suivant :
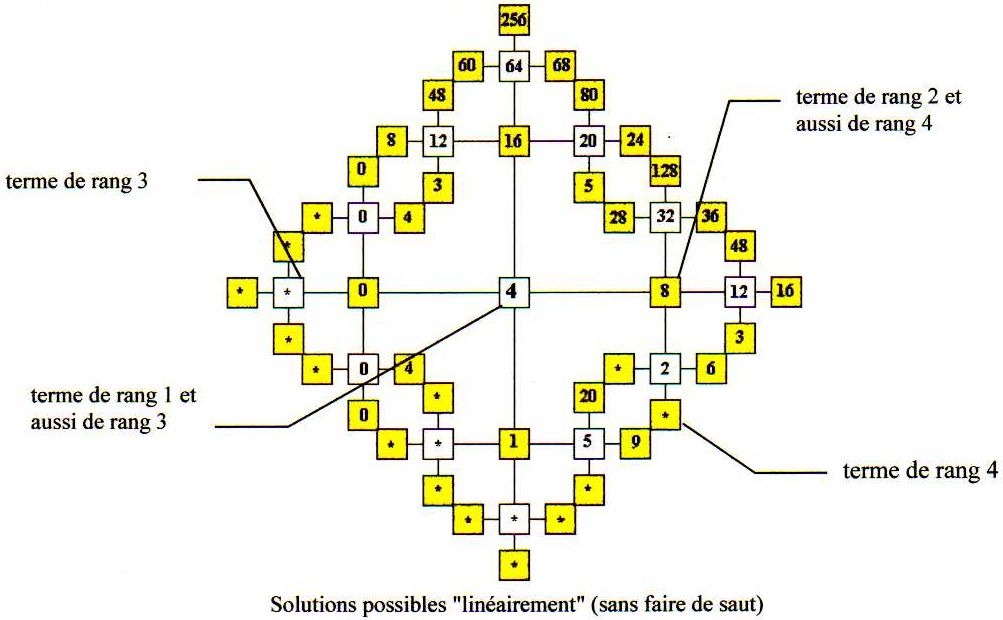
Les solutions évidentes sont celles de la dernière arborescence.
Je les ai baptisé « termes de rang 4 » car pour y accéder, nous combinons le chiffre 4 quatre fois (à partir du centre où je compte « un »).
Les termes de rang 2 sont aussi des termes de rang 4 : si nous faisons deux opérations contraire (par exemple ajouter puis enlever), nous retombons sur eux.
Mais deux nombres demandés dans l’énoncé restent absents : 7 et 32 !
En effet, ce mandala nous permet seulement de représenter les résultats des opérations effectuées les unes à la suite des autres.
Pourtant, nous pouvons combiner ensemble des termes de rang 2. Par exemple, avec 7 et 1, nous pouvons fabriquer 8. Nous retrouvons nos quatre « briques » élémentaires : 0, 1, 8 et 16.
Voilà un tableau qui donne les réponses qui nous manquait :
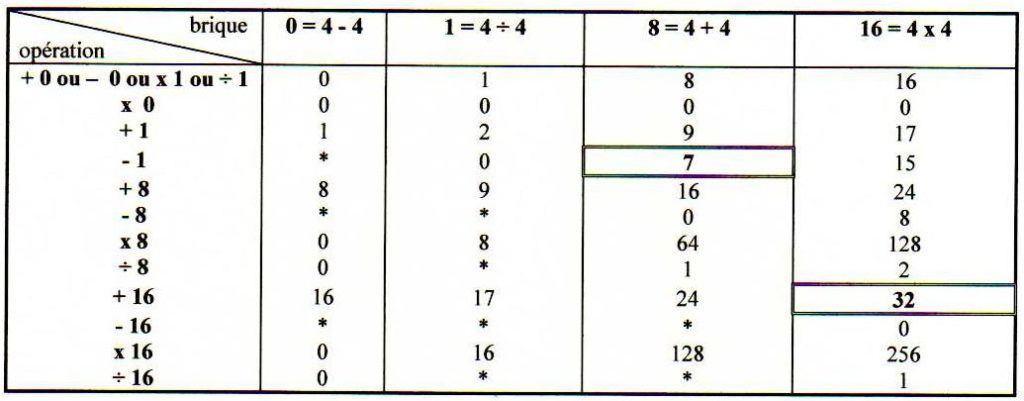
D’où : 7 = 8 – 1 soit 7 = (4 + 4) – (4 ÷ 4) et 32 = 16 + 16 soit 32 = (4 x 4) + (4 x 4).
La 1ère ligne du tableau indique les 4 « briques » ou les termes de rang 2 du mandala.
La 1ère colonne indique les 16 opérations possibles avec ces 4 « briques » ou termes de rang 2.
Nous pouvons dire que le tableau synthétise toutes les opérations possibles entre les termes de rang 2.
La combinaison du mandala avec le tableau donne toutes les réponses possibles des combinaisons de quatre nombres identiques (ici 4).
Il serait possible de faire un mandala englobant le mandala et le tableau décrit. Toutefois, à partir des termes de rang 2 (les « briques »), il y aurait 12 directions supplémentaires à indiquer. Cela est difficilement représentable sur l’espace plan de la feuille, ou en tout cas, bien incommode.
En tout cas, toutes les réponses possibles sont listées, ce qui nous permet de créer d’autres grilles de jeu comme la suivante :

Conclusion : le mandala peut être un bon outil pratique en mathématiques.
J’accueille vos commentaires et vos façons de résoudre ce jeu.
© F.C. Rava-Reny, 15/09/1998 – Article publié dans Intelligence mode d’emploi, Orthopédagogie, Gestion Mentale, Éducation, n°1, novembre 2003.
[1] Pierre Berloquin, 100 jeux numériques, Livre de Poche n°7794.
[2] Terme de chimie : partir du produit final pour remonter aux réactifs de départ, en se servant éventuellement de stades intermédiaires où existent des espèces chimiques en partie abstraite : les synthons.
